1.北斗信号服务
北斗系统具备导航定位和通信数传两大功能,提供其中服务。具体包括:面向全球范围,提供定位导航授时(RNSS)、全球短报文通信(GSMC)和国际搜救(SAR)三种服务;在中国及周边地区,提供星基增强(SBAS)、地基增强(GAS)、精密单点定位(PPP)和区域短报文通信(RSMC)四种服务。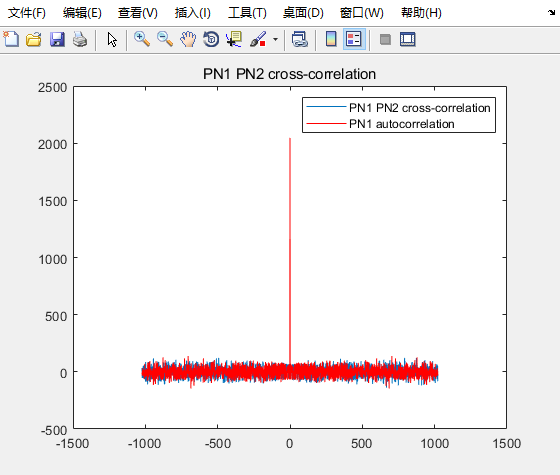
B1I 信号载波频率为 1561.098MHz,带宽为 4.092MHz,该信号在北斗二号和北斗三号的中圆地球轨道(MEO)卫星、倾斜地球同步轨道(IGSO)卫星和地球静止轨道(GEO)卫星上播发,提供公开服务。
在我学习的时候,主要使用到的是B1I上的信号,可以实现定位服务。
2. B1I信号的主要结构
B1I信号由“测距码+导航电文”调制在载波上构成,其信号表达式如下:
上角标j表示使用的卫星编号.
$A_{B1I}$表示振幅.
$C_{B1I}$表示对应的测距码.
$D_{B1I}$表示调制到B1I信号测距码上的数据码.
$f_{1}$表示载波的频率.
2.1 测距码的组成
B1I 信号测距码,也称为伪随机码,码速率为2.046Mcps,码长为 2046。𝐶𝐵1𝐼码周期为(1s/2.046Mcps)*2046 = 1ms。
B1I测距码又两对11级m序列构成(可以理解为伪随机序列)组成,其具体的结构如下图所示: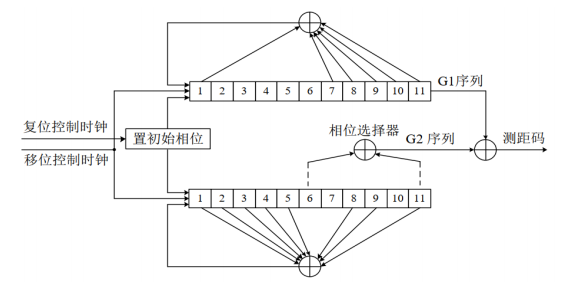
G1,G2序列的生成多项式如下:
$G1(X) = 1 + X + 𝑋^7 + 𝑋^8 + 𝑋^9 + 𝑋^{10} + 𝑋^{11}$
$G2(X) = 1 + X + 𝑋^2 + 𝑋^3 + 𝑋^3 + 𝑋^5 + X^8 + X^9 + 𝑋^{11}$
并且两个线性序列 G1 和G2 模二加(异或)产生平衡 Gold 码共 2047 比特后截断最后 1 码片生成。也可以理解为,当使用上面的结构产生PN码的时候,当生成了2046个PN码之后。将会对PN码生成器进行重置。
PN码生成器的初始值为:
G1 序列初始相位:01010101010
G2 序列初始相位:01010101010
从PN码生成器的结构中可以看到,在G2序列当中,需要提取其中两个相位的值来产生用于和G1序列进行异或,从而产生PN码。这个相位选择,是根据具体的选取的卫星来确定的,也就是说没一组卫星将会产生唯一的PN码。
常用的卫星组合如下表所示。比如卫星1号和3号,卫星1号和4号。每一组相位的选择会对应不同的PN码产生。1
2
3
4BDB1ICAlist = [ 1 3; 1 4; 1 5; 1 6; 1 8; 1 9; 1 10; 1 11; 2 7; ...
3 4; 3 5; 3 6; 3 8; 3 9; 3 10; 3 11; 4 5; 4 6; ...
4 8; 4 9; 4 10; 4 11; 5 6; 5 8; 5 9; 5 10; 5 11; ...
6 8; 6 9; 6 10; 6 11; 8 9; 8 10; 8 11; 9 10; 9 11; 10 11];
2.2 使用Matlab模拟PN码的生成
使用Matlab能够比较方便地来模拟PN码的生成理解上面的原理之后,实现起来还是比较简单的。主要就是根据伪随机码的生成规则来生成对应的PN码就可以了。
1 | function [pn_code, pn_code_sample] = PNCode_Gen(pn_code_len, samp_len, code_rate, samp_rate, pn_index) |
3.相关
对于一个随机序列,其具有良好的自相关性,一个序列的自相关函数的定义如下:
自相关函数从形式上来看有点类似与卷积的形式,简单来理解就是对于一个随机序列,对其进行自相关,也就相当于将这个函数进行滑动想成再求和,在这个过程当中,会出现一个相关的峰值,也就是当两个序列完全重合的时候会达到这个峰值。
在北斗卫星系统的B1I信号中,PN码是一种特殊的码,它具有良好的自相关性,并且该码是可以认为规定的周期序列,且能够较好地满足随机序列的分布特性。
使用PN码的另一个好处就是,它具有良好的自相关性,因此在发送端对原始的信号进行PN码调制,在接受端对接受到的信号进行PN码自相关,这样能够将原始的信号得到一个明显的增益,从而能够将原始信号从信号中提取出来。
为了能够演示PN码的自相关性和互相关性,可以对前面实现的PN码函数进行简单的测试,测试其自相关性和互相关性。其matlab测试代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58clc;
clear all;
close all;
PN_CODE_LEN = 2046; % PN Code length
CODE_RATE = 2.046e6; % standard pn code rate
SAMP_RATE = CODE_RATE*4; % sample rate
SAMP_LEN = (SAMP_RATE/CODE_RATE)*PN_CODE_LEN;
PN_INDEX1 = 8 ; % choose satellites
PN_INDEX2 = 10; % choose satellites
% generate 1 PN code, and response samples
[pn1, pn1_sample] = PNCode_Gen(PN_CODE_LEN, SAMP_LEN, CODE_RATE, SAMP_RATE, PN_INDEX1);
[pn2, pn2_sample] = PNCode_Gen(PN_CODE_LEN, SAMP_LEN, CODE_RATE, SAMP_RATE, PN_INDEX2);
% autocorrelation test
pn1_r = pn1;
pn1_shift = [pn1(1024:end), pn1(1:1023)];
pn1_autocorrelation = zeros(1, PN_CODE_LEN);
for i = 1:PN_CODE_LEN
pn1_autocorrelation(i) = sum(pn1_shift .* pn1_r);
pn1_shift = [pn1_shift(2:end), pn1_shift(1)];
end
figure(1);
plot(-1023:1:1022, pn1_autocorrelation);
title("PN1 autocorrelation")
% cross-correlation test
pn2_shift = [pn2(1024:end), pn2(1:1023)];
pn1_pn2_cross_correlation = zeros(1,PN_CODE_LEN);
for i = 1:PN_CODE_LEN
pn1_pn2_cross_correlation(i) = sum(pn2_shift .* pn1_r);
pn2_shift = [pn2_shift(2:end), pn2_shift(1)];
end
figure(2);
plot(-1023:1:1022, pn1_pn2_cross_correlation);
hold on;
plot(-1023:1:1022, pn1_autocorrelation, '-r');
legend('PN1 PN2 cross-correlation','PN1 autocorrelation');
title("PN1 PN2 cross-correlation");
% sample autocorrelation test
pn1_sampe_r = pn1_sample;
pn1_sample_shift = [pn1_sample(4092:end), pn1_sample(1:4091)];
pn1_sample_autocorrelation = zeros(1, PN_CODE_LEN);
for i = 1:SAMP_LEN
pn1_sample_autocorrelation(i) = sum(pn1_sample_shift .* pn1_sampe_r);
pn1_sample_shift = [pn1_sample_shift(2:end), pn1_sample_shift(1)];
end
figure(3);
plot( -4092:1:4091 ,pn1_sample_autocorrelation);
title("PN1 sample autocorrelation")
首先可以看标准的PN码自相关的结果,如下图所示: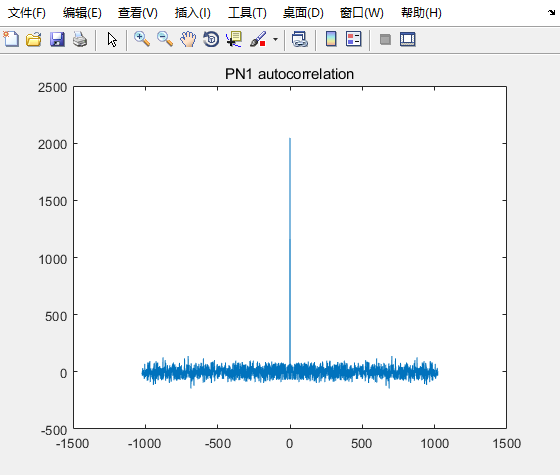
可以看到,PN码自相关的结果,只有一个比较明显的峰值。
然后我们可以看看不同PN码之间进行互相关的结果:
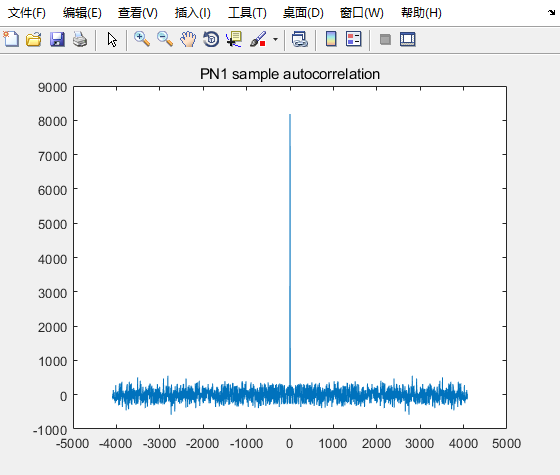
最后我们可以看以下,实际采样得到的PN码的采样点的自相关结果: