前言
最近帮一个客户实现将一部分算法卸载到FPGA上,其中的一个部分是相关算法。相关简单来说就是一个乘累加的过程。如果在设计的的时候采用一些特殊的序列,比如PN码,那么甚至可以把乘法变成加减法来进行操作。
相关运算原理
相关运算的数学表达式如下
在实际处理的时候,我们一般是使用有限长的两个序列进行相关,假设两个序列的长度为N,则上面的可以转换为:
下面以一个具体的例子来说明卷积运算的这个过程:
我们假设要进行相关的序列的长度是1024,其中绿色部分我们可以看做是具体的系数,蓝色部分是实际的要处理的数据流,当i=0的时候,需要将x0~x1023分别与h0~h1023对应相乘,然后将这1024个乘积进行累加,得到第一个相关点的结果。
当i=1,也就是相当于数据流已经流过一个点,然后再执行上面的操作计算得到第二个相关点的结果。
依次类推下去,这样我们就能得到对应的相关结果了。
PN码
在之前的博客当中,已经学习过PN码,并且了解到PN码的伪随机性,通过对PN码进行相关,能够检测到一个相关峰。
==PN码以及生成多项式==
使用python实现互相关与自相关操作
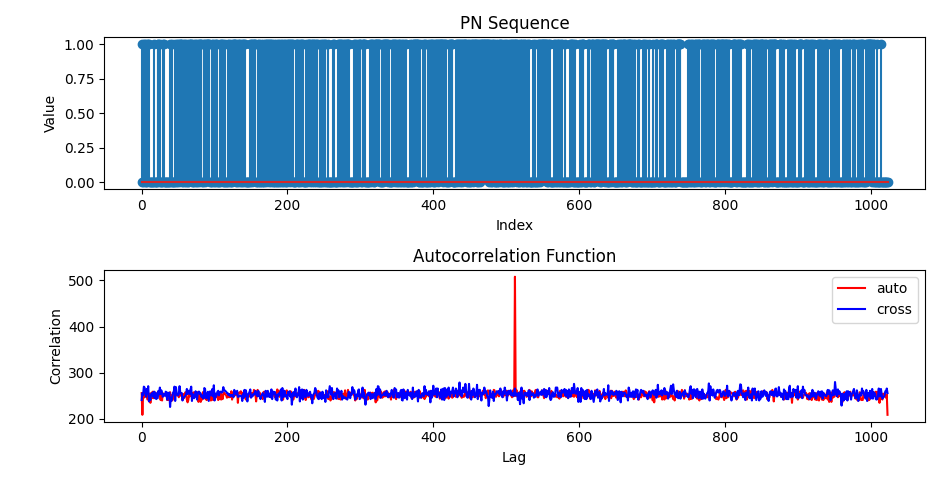
下面是一个简单的python脚本,能够实现PN码的互相关与自相关。并且能够检测到峰值。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
import numpy as np
from numpy import empty, exp, pi, arange, int8, fromiter, sum
import matplotlib.pyplot as plt
def pnsequence(pn_order, pn_seed, pn_mask, seq_length):
"""
Generate a PN (Pseudo-Noise) sequence using a Linear Feedback Shift Register (LFSR).
Seed and mask are ordered so that:
- seed[-1] will be the first output
- the new bit computed as :math:`sum(shift_register & mask) % 2` is inserted in shift[0]
Parameters
----------
pn_order : int
Number of delay elements used in the LFSR.
pn_seed : iterable providing 0's and 1's
Seed for the initialization of the LFSR delay elements.
The length of this string must be equal to 'pn_order'.
pn_mask : iterable providing 0's and 1's
Mask representing which delay elements contribute to the feedback
in the LFSR. The length of this string must be equal to 'pn_order'.
seq_length : int
Length of the PN sequence to be generated. Usually (2^pn_order - 1)
Returns
-------
pnseq : 1D ndarray of ints
PN sequence generated.
Raises
------
ValueError
If the pn_order is equal to the length of the strings pn_seed and pn_mask.
"""
# Check if pn_order is equal to the length of the strings 'pn_seed' and 'pn_mask'
if len(pn_seed) != pn_order:
raise ValueError('pn_seed has not the same length as pn_order')
if len(pn_mask) != pn_order:
raise ValueError('pn_mask has not the same length as pn_order')
# Pre-allocate memory for output
pnseq = empty(seq_length, int8)
# Convert input as array
sr = fromiter(pn_seed, int8, pn_order)
mask = fromiter(pn_mask, int8, pn_order)
for i in range(seq_length):
pnseq[i] = sr[-1]
new_bit = sum(sr & mask) % 2
sr[1:] = sr[:-1]
sr[0] = new_bit
return pnseq
pn_order = 11
pn_seed = '11010011001'
pn_mask = '11011000011'
pn_mask1 = '11011100011'
seq_length = 1024
# Generate PN sequence
pn_sequence = pnsequence(pn_order, pn_seed, pn_mask, seq_length)
# pn_sequence[pn_sequence==0] = -1
pn_sequence_shift = np.roll(pn_sequence,seq_length//2)
print("pn_sequence:", pn_sequence[:20])
pn_sequence1 = pnsequence(pn_order, pn_seed, pn_mask1, seq_length)
# pn_sequence1[pn_sequence1==0] = -1
pn_sequence_shift1 = np.roll(pn_sequence1,seq_length//2)
print("pn_sequence1:", pn_sequence1[:20])
# Calculate autocorrelation function
# acf = np.correlate(pn_sequence, np.hstack((pn_sequence[32:], pn_sequence[:32])), mode='full')
acf_auto = np.zeros(seq_length)
acf_cross = np.zeros(seq_length)
for i in range(seq_length):
acf_auto[i] = np.sum(pn_sequence * pn_sequence_shift);
acf_cross[i] = np.sum(pn_sequence * pn_sequence_shift1);
pn_sequence_shift = np.roll(pn_sequence_shift,1)
pn_sequence_shift1 = np.roll(pn_sequence_shift1,1)
# Plot results
fig, (ax1, ax2) = plt.subplots(nrows=2, ncols=1)
ax1.stem(pn_sequence)
ax1.set_title('PN Sequence')
ax1.set_xlabel('Index')
ax1.set_ylabel('Value')
ax2.plot(acf_auto,'r', label="auto")
ax2.plot(acf_cross,'b', label="cross")
ax2.legend(loc="upper right")
ax2.set_title('Autocorrelation Function')
ax2.set_xlabel('Lag')
ax2.set_ylabel('Correlation')
plt.tight_layout()
plt.show()
out_seq = pnsequence(pn_order, pn_seed, pn_mask, seq_length)
try:
with open('pn_sequence.txt', 'w') as f:
for item in out_seq:
f.write("%s\n" % item)
except Exception as e:
print("An error occurred while writing the file: ", e)
使用FPGA实现相关运算
在前面我们已经简单介绍了相关运算的原理,有了前面的介绍,想必在FPGA当中实现相关运算就有了一个大概的思路了。在FPGA当中想要实现相关操作的主要的限制是FPGA上的资源限制,比如DSP和查找表资源。如果相关的长度比较长的话,如果需要进行乘法运算,那么需要耗费大量的DSP资源。以我所使用的ZYNQ7020为例,一共只有220个DSP,因此在一些计算密集的应用当中,需要更高端的FPGA才能实现。
前面我们介绍了PN码的相关操作,可以看到PN码只是01010这种的bit。通过这种bit我们就能够实现相关,在实际使用的时候,我们也会经常遇到只需要数据的符号位就可以进行相关的情况。因此我们在FPGA当中就可以把乘法运算变成加减法运算。
然后我们还要注意的就是FPGA在进行相关运算的时候需要进行一定长度的累加,比如上面的相关的长度是1024,那么就需要进行1024个长度的累加。这么多数量的累加,想要在一个时钟周期内全部实现是不太现实的。因此我们需要实现一个模块,专门来实现1024个点的累加操作。
FPGA实现累加树
下面以一个9个数相加的过程来详细描述这个过程:
第一个时钟周期:
首先,我们有d0~d8一共9个数需要累加,在进行第一轮加法的时候,我们需要两两进行相加,可以看到一个可以进行4组加法,然后剩余了一个数据。那么在这一个时钟周期,我们需要完成4个加法和一个寄存。第二个时钟周期:
在上一个时钟周期结束之后,我们一共能够得到5个数据,继续执行两两相加,可以看到这里可以执行2组加法,剩余一个数据需要寄存。第三个时钟周期:
在上一个时钟周期结束之后,我们得到了3个数据,继续执行两两相加,执行一组加法,剩余一个数据需要寄存。第四个时钟周期
在第四个时钟周期当中,只剩下最后两个数据需要进行相加,我们就可以得到最终的结果。
假设:本次待相加的数目为n
(1) 本次需要进行的加法运算共有[n/2]组,也就是需要[n/2]的加法器,需要的寄存器的数目为[n/2] + n%2(其中[n/2]表示取整,n%2表示取余)
(2) 下一次运算需要相加的数目为[n/2] + n%2
(3)每一级的运算需要一个时钟周期的开销
因此采用递归的方式,来完成这个运算是再方便不过了。但是在C/C++或其他高级语言中使用递归是在方便不过的事情了,但是在FPGA中想要使用递归还是有点麻烦的,这时候就需要灵活的使用generate语句,来在每一级生成不同的电路。
下面是使用systemverilog实现的这个累加树的模块。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
module add_tree_impl #(
//==========================================
//parameter define
//==========================================
parameter DATA_NUM = 1024 ,//需要相加的个数
parameter HALF_IDX = DATA_NUM >> 1 ,//两两相加的个数
parameter DATA_NUM_NEW = (DATA_NUM >> 1) + (DATA_NUM%2) ,//下一级模块需要相加的个数
parameter DW = 8 ,//本阶段的输入数据位宽
parameter DW_NEW = DW + 1 ,//本阶段的输出数据位宽
parameter DWO = DW + clogb2(DATA_NUM-1) // 最终输出结果的位宽
)(
input wire clk ,
input wire rst ,
input wire pi_dv ,
input wire [DW-1: 0] pi_data [DATA_NUM-1:0] ,
output wire po_dv ,
output wire [DWO - 1 : 0] po_data
);
generate
genvar i;
reg [(DW_NEW) - 1 : 0] sum_tmp [DATA_NUM_NEW-1:0];
reg tmp_dv ;
//当前不是最后一次加法
if (DATA_NUM != 2) begin
for(i = 0; i < HALF_IDX; i = i + 1)
begin: cal_sum
always @(posedge clk) begin
if (rst==1'b1) begin
sum_tmp[i] <= 'd0;
tmp_dv <= 1'b0;
end
else begin
//两数相加,位宽扩充一位
//eg:sum_tmp[0] = pi_data[1] + pi_data[0];
//eg:sum_tmp[1] = pi_data[3] + pi_data[2];
//eg:sum_tmp[2] = pi_data[5] + pi_data[4];
//eg:sum_tmp[3] = pi_data[7] + pi_data[6];
sum_tmp[i] <= {pi_data[(2*i + 1)][DW-1],pi_data[(2*i + 1)]} + {pi_data[2*i][DW-1], pi_data[2*i]};
tmp_dv <= pi_dv;
end
end
end
//递归调用求和模块,将本季求和计算得到的模块,传递到下一级
add_tree_impl #(
.DATA_NUM(DATA_NUM_NEW),
.DW(DW_NEW)
) inst_add_tree (
.clk (clk),
.rst (rst),
.pi_dv (tmp_dv),
.pi_data (sum_tmp),
.po_dv (po_dv),
.po_data (po_data)
);
end
//==========================================
//当前需要相加的个数为奇数个需要将最后一个数据缓存
//==========================================
if (DATA_NUM%2 ==1) begin
always @(posedge clk) begin
if (rst==1'b1) begin
sum_tmp[(DATA_NUM_NEW - 1)] <= 'd0;
end
else begin
sum_tmp[(DATA_NUM_NEW - 1)] <= {pi_data[DATA_NUM-1][DW-1],pi_data[DATA_NUM-1]};
end
end
end
endgenerate
generate
//执行最后一次加法,只剩下两个数相加
if (DATA_NUM == 2) begin
reg tmp_dv_final ;
reg [DWO-1 : 0] sum_tmp_final ;
always @(posedge clk) begin
if (rst==1'b1) begin
sum_tmp_final <= 'd0;
tmp_dv_final <= 1'b0;
end
else begin
sum_tmp_final <= {pi_data[0][DW-1], pi_data[0]} + {pi_data[1][DW-1], pi_data[1]};
tmp_dv_final <= pi_dv;
end
end
assign po_dv = tmp_dv_final;
assign po_data = sum_tmp_final;
end
endgenerate
function integer clogb2;
input integer depth;
for (clogb2=0; depth>0; clogb2=clogb2+1)
depth = depth >> 1;
endfunction
endmodule
FPGA实现相关操作
前面我们实现了累加树的操作,有了上面的累加树,我们就可以实现一定个数的数据相加,并得到相加的结果。想要在FPGA上实现相关操作,接下来我们可以来实现”乘法”这一步,在本博客当中,主要是以PN码来进行的,因此是执行相关操作。
在FPGA上有一个用于相关的序列,序列的值是-1,+1。现在有输入的IQ数据的值,我们只需要有用符号位来进行相关就可以。如果符号位与序列相同,那么”乘法”的结果就为1,如果符号位与序列不同,那么”乘法”的结果就为-1,最终将所有得到的结果累加起来就可以了。
下面是使用systemverilog实现这个功能的模块。
1 | module cross_correlation#( |